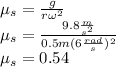Question

A mass m is placed on the inside surface of a vertical cylinder that is rotating about its central axis. If the radius of the cylinder is 0.5 m and the angular velocity of the cylinder is 6 rad/s, what minimum value of µs (the coefficient of static friction) is required to keep the mass from slipping down the wall of the cylinder?

Answer 1

`\mu_s=0.54`

Step-by-step explanation:

In order for the friction to be sufficient to keep the mass from falling, the force of gravity (mg) must be the same friction force(
`f_s`) and the centripetal force (
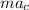`ma_c`) must to have the same value of the normal force (N):

`mg=f_s\\N=ma_c`

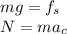
Recall that
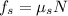`f_s=\mu_sN`, so we have:

`f_s=mg\\f_s=\mu_sma_c\\\mu_sma_c=mg\\\mu_s=(g)/(a_c)`

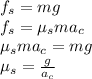
Recall that
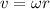`v=\omega r`. The centripetal acceleration is given by:

`a_c=(v^2)/(r)\\a_c=r\omega^2`

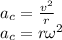
Finally, replacing
`a_c`:

`\mu_s=(g)/(r\omega^2)\\\mu_s=(9.8(m)/(s^2))/(0.5m(6(rad)/(s))^2)\\\mu_s=0.54`