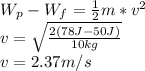Question

Paul’s 10 kg baby sister Susan sits on a mat. Paul pulls the mat across the floor using a rope that is angled 30° above the floor. The tension is a constant 30 N and the coefficient of kinetic friction is 0.20. Use work and energy to find Susan’s speed after being pulled 3.0 m.

Answer 1

Answer: speed= 1.95866m/s ~= 2.0 m/s

Explanation: check attachment for explanation

Answer 2

The speed of Susan is 2.37 m/s

Step-by-step explanation:

To visualize better this problem, we need to draw a free body diagram.

the work is defined as:

`W=F*d*cos(\theta)`

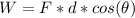
here we have the work done by Paul and the friction force, so:

`W_p=F_p*d*cos(0)\\F_p=30N*cos(30^o)=26N\\W_p=26*3*(1)=78J`

`W_f=F_f*d*cos(180)\\F_f=\µ*(10*9.8-30N*sin(30^o))=16.6N\\W_p=16.6*3*(-1)=50J`

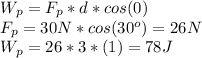
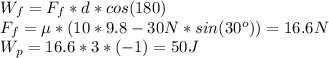
Now the change of energy is:

`W_p-W_f=(1)/(2)m*v^2\\v=\sqrt{(2(78J-50J))/(10kg)}\\v=2.37m/s`