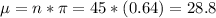Question

Gallagher et al. (A-6) reported on a study to identify factors that influence women's attendance at cardiac rehabilitation programs. They found that by 12 weeks post-discharge, only 64 percent of eligible women attended such programs. Use 64 percent as the attendance percentage of all eligible women. For random samples of 45 women, what is the mean and standard error of the sampling distribution of the sample proportion of women who attend such programs? Round your answer to two decimal places.

Answer 1

The mean is 28.8 women with a standard error of 0.07.

Explanation:

For each women studied, there are only two possible outcomes. Either they attended such programs, or they didn't. This means that we can solve this problem using concepts of the binomial probability distribution.

Binomial distribution:

We measure the probability of exactly x sucesses on n repeated trials, with
`\pi` probability.

The mean is given by:

`\mu = n*\pi`

The standard error is given by:

`s = \sqrt{(\pi(1-\pi))/(n)}`

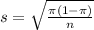
In this problem, we have that:

Use 64 percent as the attendance percentage of all eligible women. This means that
`\pi = 0.64`.

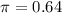For random samples of 45 women, what is the mean and standard error of the sampling distribution of the sample proportion of women who attend such programs?

Our sample has 45 women, so
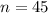`n = 45`.

`\mu = n*\pi= 45*(0.64) = 28.8`

`s = \sqrt{(\pi(1-\pi))/(n)} = \sqrt{(0.64*(0.36))/(45)} = 0.07`