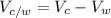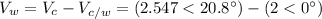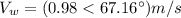Answer:
Vw = 0.98m/s due 67.16° north of east
Step-by-step explanation:
The distance the canoeist wants to travel is:

And the angle of the destination point is
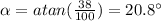
With this trajectory and the time of 42s, we get the velocity of the canoe respect to ground:
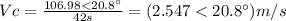
Now we can calculate the velocity of the water: