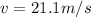Question

While standing at the edge of the roof of a building, a man throws a stone upward with an initial speed of 7.19 m/s. The stone subsequently falls to the ground, which is 20.1 m below the point where the stone leaves his hand. At what speed does the stone impact the ground? Ignore air resistance and use ????=9.81 m/s² for the acceleration due to gravity.

Answer 1

21.1 m/s

Step-by-step explanation:

The motion of the stone is a uniformly accelerated motion (free fall), so we can find the final velocity of the stone by using the following suvat equation

`v^2-u^2=2as`

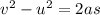
where

v is the final velocity

u is the initial velocity

a is the acceleration

s is the vertical displacement

For the stone in this problem, taking upward as positive direction, we have:

u = +7.19 m/s is the initial velocity

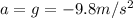`a=g=-9.8 m/s^2` is the acceleration of gravity

s = -20.1 m is the displacement

Solving for v, we find the final velocity:

`v=√(u^2+2as)=√((7.19)^2+2(-9.8)(-20.1))=\pm 21.1 m/s`

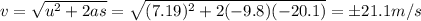
And the correct solution is the one with negative sign, since the final velocity is downward:

`v=-21.1 m/s`

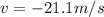
Therefore, the final speed (the magnitude of the velocity) is

`v=21.1 m/s`