Question

The daily profit P ​(in thousands of​ dollars) from the sale of televisions is a function of the number x of televisions sold ​(in hundreds).

The formula for this function​ is:
P​ = -5x² + 13x - 4
What are the​ break-even sales amounts​ (the sales amounts that result in no profit or​ loss)?

Answer 1

The break-even sales amounts​ is 36 or 224.

Explanation:

Consider the provided function.

`P= -5x^2 + 13x - 4`

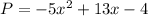
Where x is the number of televisions sold (in hundreds) and P is the profit.

We need to calculate the break-even sales amounts​.

the​ break-even sales amounts​ is the sales amounts that result in no profit or​ loss.

That means substitute P=0 and solve for x.

`-5x^2 + 13x - 4=0`

`5x^2-13x+4=0`

`\mathrm{For\:a\:quadratic\:equation\:of\:the\:form\:}ax^2+bx+c=0\mathrm{\:the\:solutions\:are\:}\\x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`

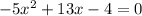
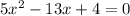
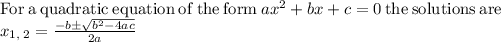
Substitute a=4, b=-13 and c=4 in above formula.

`x_(1,\:2)=(-\left(-13\right)\pm √(\left(-13\right)^2-4\cdot \:5\cdot \:4))/(2\cdot \:5)`

`x_(1,\:2)=(13\pm√(169-80))/(10)`

`x_(1,\:2)=(13\pm√(89))/(10)`

`x=(13+√(89))/(10),\:x=(13-√(89))/(10)\\x\approx2.243, \ or\ x\approx 0.357`

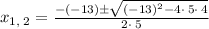
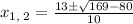
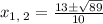
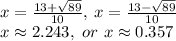
Therefore, the break-even sales amounts​ is 36 or 224.