Answer:
(-30,-3)
Explanation:
The given system is
7x-6y=-192
10y=x
Substitute the bottom equation into the top equation to obtain:
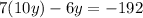
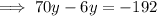
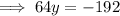
Divide both sides by 64
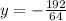
y=-3
This implies that:
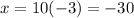
The point of intersection is the solution to the two systems.
The lines intersected at: (-30,-3)