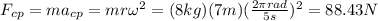Answer:
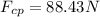
Step-by-step explanation:
The equation for centripetal force is given by Newton's 2nd Law:
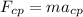
The equation for centripetal acceleration is
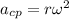
If the object makes one revolution (an angle of
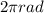 ) every 5 seconds it means that its angular velocity is
) every 5 seconds it means that its angular velocity is
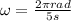 .
.
Putting all together, and for our values: