Question

PLZ Help as fast as you can:)

Find some examples of real-world triangles in a similar way, and find approximate distances using the Triangle Proportionality Theorem. Post your findings and explain how you used Triangle Proportionality Theorem.

Answer 1

any options to choose from?

or go to edubirdy and search it and it will definitely help you out

Answer 2

The Triangle Proportionality Theorem is about the similarity between a pair of triangles, where corresponding pair of sides are proportional and corresponding pairs of angles are congruent.

An real-wold situation where we use this theorem is when we use the shadow and height of an small object to find the height of a bigger object. For example, the image attached shows a tree and a bulding, we know the length of the height and shadow of the tree, and we also know the shadow length of the building. So, we want to measure indirectly the height of the building, to do that, we apply the triangle proportionality theorem, which is the following proportion

`(y)/(x)=(h)/(s)`

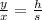
You can obser that each ratio is about a specific triangle, we don't mixed magnitudes from different triangles in one ration, because that can get messy. Then, we replace all given values

`(y)/(12.5m)=(2m)/(2.5m) \\y=(2(12.5)m)/(2.5)\\ y=10m`

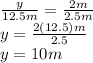
Therefore, the building is 10 meters tall.

So, there you have it, one real-world example and how we apply the theorem.