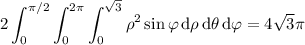Given that you mention the divergence theorem, and that part (b) is asking you to find the downward flux through the disk
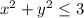 , I think it's same to assume that the hemisphere referred to in part (a) is the upper half of the sphere
, I think it's same to assume that the hemisphere referred to in part (a) is the upper half of the sphere
 .
.
a. Let
 denote the hemispherical cap
denote the hemispherical cap
 , parameterized by
, parameterized by
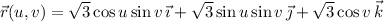
with
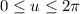 and
and
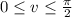 . Take the normal vector to
. Take the normal vector to
 to be
to be
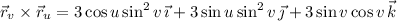
Then the upward flux of
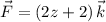 through
through
 is
is

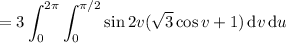
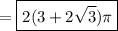
b. Let
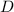 be the disk that closes off the hemisphere
be the disk that closes off the hemisphere
 , parameterized by
, parameterized by
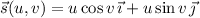
with
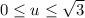 and
and
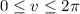 . Take the normal to
. Take the normal to
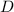 to be
to be
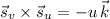
Then the downward flux of
 through
through
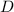 is
is
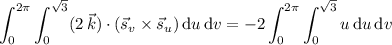
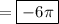
c. The net flux is then
 .
.
d. By the divergence theorem, the flux of
 across the closed hemisphere
across the closed hemisphere
 with boundary
with boundary
 is equal to the integral of
is equal to the integral of
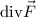 over its interior:
over its interior:
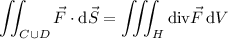
We have

so the volume integral is
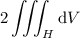
which is 2 times the volume of the hemisphere
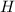 , so that the net flux is
, so that the net flux is
 . Just to confirm, we could compute the integral in spherical coordinates:
. Just to confirm, we could compute the integral in spherical coordinates: