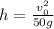Question

An apple with mass M is hanging at rest from the lower end of a light vertical rope. A dart of mass M/4 is shot vertically upward, strikes the bottom of the apple, and remains embedded in it. If the speed of the dart is v₀ just before it strikes the apple, how high does the apple move upward because of its collision with the dart?

Answer 1

The apple moves a height of
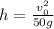`h=(v_(0)^2)/(50g)` because of its collision with the dart.

Step-by-step explanation:

First we need to calculate the velocity that the final mass gets once the collision takes place, in order to do this, we use momentum conservation.

The movement develops in a vertical line, so we use magnitudes, and inicially only the dart is moving, but finally both masses embedded are in movement. We write

`P_(i)=P_(f)\Leftrightarrow (M)/(4)v_(0)=(5)/(4)Mv`

from here, we get the value for the velocity of the final mass,
`v`, once the collision has been produced (an instant after)

`v=(v_(0))/(5)`

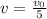
Second, with this final velocity, we can calculate the final altitude that the mass will get, to do this we use energy conservation. An instant after the collision, the mass has kinetic energy, and we say that that is our altitude zero (or potencial energy zero), but when the mass gets to its higher altitude, the kinetic energy is zero and the potencial energy is different than zero, so we write the following equality

`E_(i)=E_(f)\Leftrightarrow K_(i)=V_(f)\Leftrightarrow \frac{1}2}((5)/(4)M)((v_(0))/(5))^2=((5)/(4)M)gh`

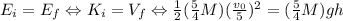
from where we clear h, and get the answer to the question.

Wich is

`h=(v_(0)^2)/(50g)`