Answer:
Height of the building = 11.4 m
Step-by-step explanation:
As we know that the stone is projected at an angle 46 degree with speed 8.65 m/s
so the two components of the speed is given as
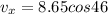
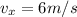
vertical component of the speed is given as
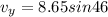
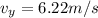
now we know that the ball strike at horizontal distance of 13.7 m
so we will have
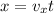
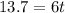
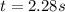
now we know that in vertical direction ball will move under uniform gravity so we can use kinematics
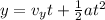

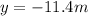
Height of the building = 11.4 m