Answer:
The correct vertex said by classmate is (-2, -6).
Solution:
Given, equation of parabola is
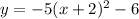
We have to find mistake did by the classmate and rectify it.
Now we know that, general form of an parabolic equation is
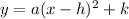
where a is an constant and (h, k) is vertex point of the parabola.
So, now by comparison of given parabola equation with general form, h = -2 and k = -6
Then, vertex point will be (-2, -6).
We can say that, classmate mistook the general form as
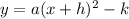
So he got h = 2 and k = 6.
Hence, the correct vertex is (-2, -6).