Question

Find the value of yy in each equation. Explain how you determined the value of yy.

a. y = log2(2^2)
b. y = log2(2^5)
c. y = log2(2^−1)
d. y = log2(2^x)

Answer 1

a) 2

b) 5

c) -1

d) x

Explanation:

We know the properties of log function as:

1) log(AB) = log(A) + log(B)

2)
`\log((A)/(B)) = \log(A)+\log(B)`

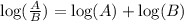
3) log(aᵇ) = b × log(a)

also,

4)
`\log_b(a)=(\log(a))/(\log(b))`

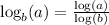
Given:

a. y = log₂(2²)

thus, using 3

y = 2log₂(2)

or using 4

y = 2 ×
`(\log(2))/(\log(2))`

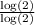
or

y = 2 × 1 = 2

b. y = log₂(2⁵)

thus, using 3

y = 5 × log₂(2)

or using 4

y = 5 ×
`(\log(2))/(\log(2))`

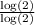
or

y = 5 × 1 = 5

c. y = log₂(2⁻¹)

thus, using 3

y = -1 × log₂(2)

or using 4

y = -1 ×
`(\log(2))/(\log(2))`

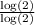
or

y = -1 × 1 = -1

d. y = log₂(2ˣ)

thus, using 3

y = x × log₂(2)

or using 4

y = x ×
`(\log(2))/(\log(2))`

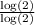
or

y = x × 1 = x