Question

Two automobiles of equal mass approach an intersection. One vehicle is traveling with velocity 10.9 m/s toward the east, and the other is traveling north with velocity v2i. Neither driver sees the other. The vehicles collide in the intersection and stick together, leaving parallel skid marks at an angle of 57.9° north of east. The speed limit for both roads is 35 mi/h, and the driver of the northward-moving vehicle claims he was within the limit when the collision occurred. Is he telling the truth?

Answer 1

Answer:False

Step-by-step explanation:

Given

first vehicle velocity is 10.9 m/s due to east

let second vehicle velocity be
`v_y` due to north

safe limit
`=35 mi/h\approx 15.64 m/s`

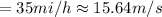
It is given that Final velocity makes an angle of
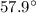`57.9^(\circ)` w.r.t to east

let
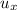`u_x` and
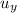`u_y` be the final velocity after collision

Conserving momentum in x direction

`m* 10.9=2m* u_x`

`u_x=(10.9)/(2)`

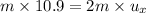
Conserving momentum in y direction

`m* v_y=2m* u_y`

`u_y=(v_y)/(2)`

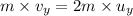
and thus
`\tan \theta =(u_y)/(u_x)`

`\tan (57.9)=(v_y)/(10.9)`

`v_y=17.37 m/s`

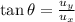
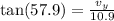
But maximum velocity within safe limit is 15.64 m/s

thus Claim of driver moving towards north is false