Question

1) find the equation of the line parallel to

x-5y=6 and through (4,-2).



2) find the equation of the line perpendicular to y= -2/5x + 3 and through (2,-1)


PLEASE ANSWER THANK YOU SO MUCH!!

Answer 1

1) The equation of the line parallel to x-5y=6 and through (4,-2) is 5y = x -14

2) The equation of the line perpendicular to y= -2/5x + 3 and through (2,-1) is 2y = 5x -12

Solution:

1) find the equation of the line parallel to x-5y=6 and through (4,-2).

Given, line equation is x – 5y = 6

We have to find the line equation that is parallel to given line and passing through the point (4, -2)

Now, let us find slope of the given line.

`\text { Slope }=\frac{-x \text { coefficient }}{y \text { coefficient }}=(-1)/(-5)=(1)/(5)`

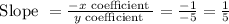
Now, we know that, slope of parallel lines are equal.

So, slope of required line is 1/5 and it passes through (4, -2)

Now, using point slope form

`y-y_(1)=m\left(x-x_(1)\right) \text { where } m \text { is slope and }\left(x_(1), y_(1)\right) \text { is point on line. }`

`y-(-2)=(1)/(5)(x-4) \rightarrow 5(y+2)=x-4 \rightarrow 5 y+10=x-4 \rightarrow x-5 y=14`

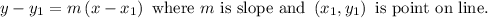
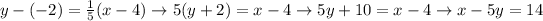
Hence, the line equation is 5y = x -14

2) find the equation of the line perpendicular to y= -2/5x + 3 and through (2,-1)

`\text { Given, line equation is } y=-(2)/(5) x+3 \rightarrow 5 y=-2 x+15 \rightarrow 2 x+5 y=15`

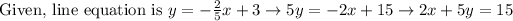
We have to find the line equation that is perpendicular to given line and passing through the point (2, -1)

Now, let us find slope of the given line.

`\text { Slope }=\frac{-x \text { coefficient }}{y \text { coefficient }}=(-2)/(5)=-(2)/(5)`

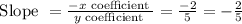
Now, we know that, product of slopes of perpendicular lines equals to -1.

So, slope of required line
`*` slope of given line = -1

slope of required line =
`-1 * (5)/(-2)=(5)/(2)`

And it passes through (2, -1)

Now, using point slope form

`\begin{array}{l}{\text { Line equation is } y-(-1)=(5)/(2)(x-2) \rightarrow 2(y+1)=5(x-2)} \\\\ {\rightarrow 2 y+2=5 x-10 \rightarrow 5 x-2 y=12}\end{array}`

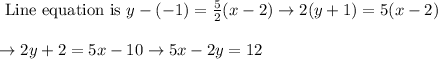
Hence, the line equation is 2y = 5x -12