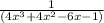Answer:
The simplication of x-3÷4x^4-8x^3-18x^2+17x+3 is
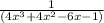
Solution:
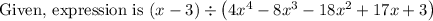
Now we have to simplify the given expression,
For that, we have to factorize the denominator.
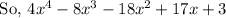
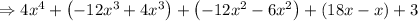
By grouping terms we get,
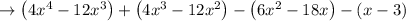
By taking the common terms,
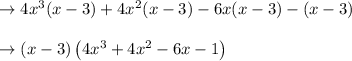
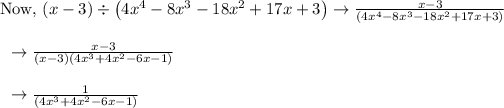
Hence, the simplified expression is