Question

Given that a rectangle has a length of 5/2x + 10 with a width of 5/2x + 5, which expression represents the area of the rectangle?

A. 25x^2/2 + 75x/2 + 50

B. 25x^2/4 + 75x/4 + 50

C. 25x^2/4+ 75x/2+ 50

D. 25x^2/2 + 75x/4 + 50

Answer 1

Option C. 25x^2/4+ 75x/2+ 50

Explanation:

A rectangle is a figure consisting of 4 sides in total with 2 pairs of equal size, defined by a length and a width. The Rectanlge Area is defined as:

`A_(R)=wl` Eqn. (1)

where:

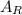`A_(R)` is the Area of Rectangle

`w` is the width

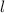`l` is the length.

Now in the given question we know the following:

`w=(5)/(2)x+5`

`l=(5)/(2)x+10`

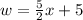
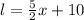
By subsitution of the above in Eqn (1) we obtain:

`A_(R) = ((5)/(2)x+5)((5)/(2)x+10)\\`

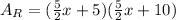
(factoring out brackets we get:)

`A_(R) = (25)/(4)x^(2)+(25)/(2)x+(50)/(2)x+50`

(gathering all same terms we get:)

`A_(R) = (25)/(4)x^(2)+(75)/(2)x+50`

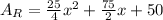
Which is the final result for
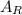`A_(R)` and by comparing with the given options in the Question, we conclude that the expression that represents the area of the rectangle is Option C.