Question

Lamar writes several equations trying to better understand potential energy. H = d with an arrow to the equation W = F d and P E Subscript g Baseline = m g h. F Subscript g Baseline = mg with arrows to the F in W = F d and to P E Subscript g Baseline = m g h. What conclusion is best supported by Lamar's work? The elastic potential energy is the same for any distance from a reference point. The gravitational potential energy equals the work needed to lift the object. The gravitational potential energy is the same for any distance from a reference point. The elastic potential energy equals the work needed to stretch the object.

Answer 1

The correct answer is B.

B. The gravitational potential energy equals the work needed to lift the object.

Step-by-step explanation:

it is correct

Answer 2

The gravitational potential energy equals the work needed to lift the object.

Step-by-step explanation:

here we know that

`H = \vec d`

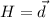
work done is given as

`W = \vec F . \vec d`

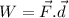
Potential energy is given as

`PE_g = mgh`

force due to gravity is given as

`\vec F_g = mg`

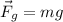
now here if we plug in the value of distance and force in the formula of work done then we will have

`W = (mg)(h)`

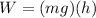
so here we got

`W = PE_g`

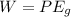
so we can concluded that

The gravitational potential energy equals the work needed to lift the object.