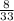Question

Find the slope of a line perpendicular to line LT if L(8,-40) and T(0,-7)​

Answer 1

The slope of the line perpendicular to LT if L(8,-40) and T(0,-7)​ is
`(8)/(33)`

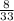
Solution:

Given, two points are L (8, -40) and T (0, -7).

We have to find the slope of the perpendicular line to the line LT.

Now let us find the slope of the line LT.

We know that, slope of line is given as

`\mathrm{m}=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { where }\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right) \text { are points on the line. }`

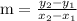
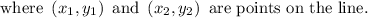
Now, slope of LT
`=(-40-(-7))/(8-0)=(-40+7)/(8)=(-33)/(8)`

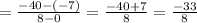
We know that, slope of line
`*` slope of perpendicular line = -1

`(-33)/(8) * \text { slope of perpendicular line }=-1`

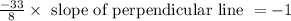
Slope of perpendicular line
`=-1 * (8)/(-33)=(8)/(33)`

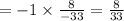
Hence, the slope of the line perpendicular to LT is
`(8)/(33)`