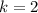Question

Given f(x) and g(x) = f(k⋅x), use the graph to determine the value of k.

Two lines labeled f of x and g of x. Line f of x passes through points negative 4, 0 and 0, 4. Line g of x passes through points negative 2, 0 and 0, 4.

-2
-1/2
1/2
2

Answer 1

k=2

Explanation:

We are given that

Line of f(x) passes through the points (-4,0) and (0,4).

Line of g(x) pass through the points (-2,0) and (0,4).

`g(x)=f(k\cdot x)`

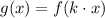
We have to determine the value of k.

`f(-4)=0`

`g(-2)=0`

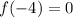
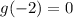
slope of f(x)=
`m=(y_2-y_1)/(x_2-x_1)=(4-0)/(0+4)=1`

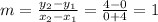
Equation of f(x) which is passing through the point (-4,0) with slope 1

`y-0=1(x+4)`

By using slope-point form:
`y-y_1=m(x-x_1)`

`y=x+4`

`g(x)=f(kx)`

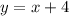
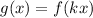
Replace x by kx

Equation of g(x)

`y=kx+4`

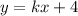
Substitute x=-2

`g(-2)=-2k+4`

`-2k+4=0`

`2k=4`

`k=(4)/(2)=2`

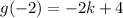
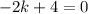
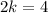
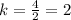
Hence, the value of
`k=2`