Question

In this sequence, term number 1 has a value of 6,

term number 2 has a value of 12, term number 3 has
a value of 22, and so on:
6, 12, 22, 36, 54, ...
If n represents the term number, demonstrate that
the rule 2n + 4 will generate the sequence.​

Answer 1

2n² + 4

Explanation:

Let,
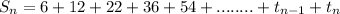`S_(n) = 6 +12 +22 +36 +54 + ........ +t_(n-1) +t_(n)` ...... (1)

Now, sift the right hand side by one term and subtract from original equation (1).

Hence, we get

(
`S_(n) -S_(n) =6+ [(12-6) + (22-12) + (36-22) + (54-36) + ....... ] - t_(n)`

⇒ tₙ = 6 + [ 6 + 10 + 14 + 18 + ........ up to (n-1)th term]

Now, the sum within the bracket is an A.P. sum.

Hence, tₙ = 6+ [
`(n-1)/(2)(2*6+(n-2)*4)`]

= 6+
`(n-1)/(2) (4n+4)`

= 6+ 2(n²-1)

= 2n² + 4

Therefore, the general term 2n² + 4 represent the sequence. (Answer)