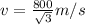Question

X2 is 8 km please help​

Answer 1

`v=(800)/(√(3) )  m/s`

Step-by-step explanation:

Given that,

A body is projected at an angle of 45°(β) with an intial elevation .

We can see that there will be no change in the horizontal component of velocity. Let the velocity of projection be v.

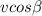`vcos\beta` would be the horizontal component.

Now we see that the time taken to decent from the maximum height of
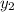`y_(2)` , the body will cover a horizontal distance of
`x_(2)`.

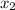At the maximum height vertical component of velocity is zero so the time taken to fall is given by:-

`vcos\beta *t=x_(2)`

`\beta =45`

`x_(2)=8000m`

`t=\sqrt{(2y_(2) )/(g) }`

`t=10√(6) s`

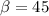
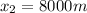
On the substituting t in abow expression we get

`v=(800)/(√(3) )  m/s`