Answer:
Width =√10 and Height =
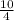
Explanation:
Let the coordinates of the vertices of the rectangle which lie on the given parabola y = 5 - x² ........ (1) are (h,k) and (-h,k).
Hence, the area of the rectangle will be (h + h) × k
Therefore, A = h²k ..... (2).
Now, from equation (1) we can write k = 5 - h² ....... (3)
So, from equation (2), we can write
![A =h^(2) [5-h^(2) ]=5h^(2) -h^(4)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/mln86d63zt2c41ogxpm4asttsebyee8wsd.png)
For, A to be greatest ,
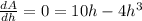
⇒
![h[10-4h^(2) ]=0](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8kmn4kjf48hgj1lchsb0orwg4pt0dd8du0.png)
⇒
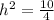 {Since, h≠ 0}
{Since, h≠ 0}
⇒ h = ±
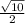
Therefore, from equation (3), k = 5 - h²
⇒
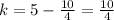
Hence, Width = 2h =√10 and Height = k =
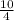 . (Answer)
. (Answer)