Question

Police often set up sobriety checkpointslong dashroadblocks where drivers are asked a few brief questions to allow the officer to judge whether or not the person may have been drinking. If the officer does not suspect a​ problem, drivers are released to go on their way.​ Otherwise, drivers are detained for a Breathalyzer test that will determine whether or not they will be arrested. The police say that based on the brief initial​ stop, trained officers can make the right decision 68​% of the time. Suppose the police operate a sobriety checkpoint after​ 9:00 p.m. on a Saturday​ night, a time when traffic safety experts suspect that about 10​% of drivers have been drinking. a) You are stopped at the checkpoint and, of course, have not been drinking. What's the probability that you are detained for further testing?b) What's the probability that any given driver will be detained?c) What's the probability that a driver who is detained has actually been drinking?d) What's the probability that a driver who was released had actually been drinking?

Answer 1

a) There is a 32% probability that you are detained for further testing.

b) There is a 35.6% probability that any given driver will be detained.

c) There is a 19.10% probability that a driver who is detained has actually been drinking.

d) There is a 4.97% probability that a driver who was released had actually been drinking.

Explanation:

We have these following probabilities:

A 10% probability that a driver has been drinking

A 90% probability that a driver has not been drinking.

A 68% probability that the officers make the right decision.

A 32% probability that the officers make the wrong decision.

a) You are stopped at the checkpoint and, of course, have not been drinking. What's the probability that you are detained for further testing?

The correct decision is that you are released. However, there is a 32% probability that the officers make the wrong decision.

This means that there is a 32% probability that you are detained for further testing.

b) What's the probability that any given driver will be detained?

90% of drivers have not been drinking. There is a 32% probability that the officers make an incorrect decision and they are detained.

10% of the drivers have been drinking. There is a 68% probability that the officers make the right decision and they are detained.

So

`P = 0.32(0.90) + 0.10(0.68) = 0.356`

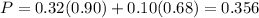
There is a 35.6% probability that any given driver will be detained.

c) What's the probability that a driver who is detained has actually been drinking?

We found out in b) that there is a 35.6% probability that a driver is detained.

Of this, those that are drinking are 68% of 10%. So

`P = (0.68*(0.10))/(0.356) = 0.1910`

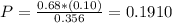
There is a 19.10% probability that a driver who is detained has actually been drinking.

d) What's the probability that a driver who was released had actually been drinking?

Either a driver has been released or he has been detained. The sum of these probabilities is 100%. There is a 35.6% probability that any given driver will be detained. So, there is a 100%-35.6% = 64.4% probability that a driver is released.

Of this, those that are drinking are 32% of 10%. So

`P = (0.32*0.10)/(0.644) = 0.0497`

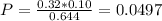
There is a 4.97% probability that a driver who was released had actually been drinking.