Question

In a circle if you have two arcs one is 60° and one is 97° are they congruent

Answer 1

Two arcs on a circle having central angle as
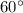`60^(\circ)` and
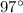`97^(\circ)` are not congruent.

Solution:

Need to find whether two arcs having central angle as
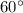`60^(\circ)` and
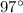`97^(\circ)` of same circle are congruent or not.

For congruency of two arcs, radius and length of the arc must be same.

Since two arcs in discussion is on same circle, so radius is equal

Let’s assume radius of circle = r

`\text { Length of the arc }=2 \pi r *\left((\theta)/(360)\right)`

where θ is central angle.

So length of the arc when central angle
`=60^(\circ)=2 \pi r * (60)/(360)=0.3333 \pi r`

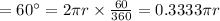
Length of the arc when central angle =
`97^(\circ)=2 \pi r * (97)/(360)=0.5388 \pi r`

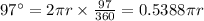
So clearly length of the two arc are not equal. Hence two arcs having central angle as
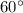`60^(\circ)` and
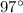`97^(\circ)` are not congruent.