Question

4. Ten bonds are purchased for $9,855.57. They are kept for 5 years and coupon payments are received at the end of each of the 5 years. Immediately following the owner’s receipt of the 5th coupon payment, the owner sells each bond for $50 less than its par value. The bond coupon rate is 8%, and the owner’s money yields a 10% annual return. Determine the face value of each bond.

Answer 1

The face value of each bond was $1,100

Step-by-step explanation:

Hi, well, first we have to assume that all the future cash flows make sense to the owner of the bonds, that is, we are assuming that he paid the fair price for all the bonds and since they were 10, the price of each bond was $9,855.57/10= $985.56.

Now, we need to find the face value of the bond, taking into account that we planned to sell the bonds $50 less than its face value, therefore the equation that we need to solve for "X" (X being the face value of the bond) is:

`Price=(Coupon((1+Yield)^(n)-1) )/(Yield(1+Yield)^(n) ) +(FaceValue-50)/((1+Yield)^(n) )`

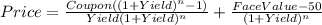
Where:

Coupon = X * 8%

Yield = owner´s money yield

n = periods of payment

X = Face Value

So, it should look like this:

`985.56=(X(0.08)((1+0.10)^(5)-1) )/(0.10(1+0.10)^(5) ) +(X-50)/((1+0.10)^(5) )`

`985.56=X(0.30326294)+X(0.62092132)-31.0460662`

`1016.6031=X(0.92418426)`

`X=1,100`

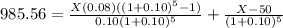
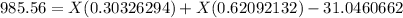
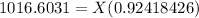
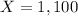
So, the face value of each bond was $1,100

Best of luck.