Question

X (5 + x) = x² + 3x + 1 find value for x

Answer 1

`\displaystyle{x=(1)/(2)}`

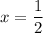
Explanation:

Given our quadratic equation:

`\displaystyle{x(5+x) = x^2 + 3x + 1}`

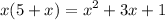
We know it's quadratic equation because we are able to tell that the highest degree of equation is 2 as seen in the equation itself.

First, we will be multiplying or simplifying the LHS (Left-Hand Side) so we can arrange the expression in standard quadratic equation form. Using distributive property, we multiply x with 5 and also with another x too, this will get us with:

`\displaystyle{x \cdot 5 + x\cdot x= x^2 + 3x + 1}\\\\\displaystyle{5x + x^2= x^2 + 3x + 1}`

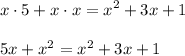
Next, we will arrange entire equation to
`\displaystyle{ax^2+bx+c=0}`:

`\displaystyle{5x+x^2= x^2 + 3x + 1}\\\\\displaystyle{x^2-x^2+5x-3x-1=0}`

Simplify:

`\displaystyle{2x-1=0}`

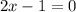
After simplifying the expression, notice that it becomes a linear equation, meaning that two parabolas only have one common point (since both equations are quadratic, both have parabola graph.)

Solve for x-term:

`\displaystyle{2x=1}\\\\\displaystyle{x=(1)/(2)}`

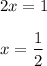
Therefore, the value of x is 1/2. We can also check the answer if the solution is correct or not by substituting the solution that we have got in the equation and see if both sides are equal or not.

If both are equal or the equation is true then it means that the solution that we have solved is correct. Otherwise, it's not.

Substitute x = 1/2 in the equation:

`\displaystyle{(1)/(2)\left(5+(1)/(2)\right)=\left((1)/(2)\right)^2+3\left((1)/(2)\right)+1}\\\\\displaystyle{(5)/(2)+(1)/(4)=(1)/(4)+(3)/(2)+1}\\\\\displaystyle{(5)/(2)-(3)/(2)=(1)/(4)-(1)/(4)+1}\\\\\displaystyle{(2)/(2)=1}\\\\\displaystyle{1=1}`

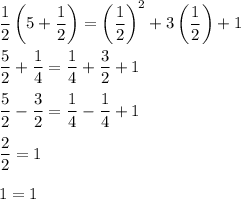
Now that both sides have same value - the equation is true when x = 1/2. Therefore, we can conclude that the solution to this equation is x = 1/2.