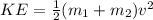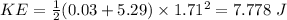Question

Assume: The bullet penetrates into the block and stops due to its friction with the block. The compound system of the block plus the bullet rises to a height of 0.15 m along a circular arc with a 0.27 m radius. Assume: The entire track is frictionless. A bullet with a m1 = 30 g mass is fired horizontally into a block of wood with m2 = 5.29 kg mass. The acceleration of gravity is 9.8 m/s 2 . 0.27 m 5.29 kg 30 g vbullet 0.15 m Calculate the total energy of the composite system at any time after the collision.

Answer 1

The total energy of the system is 7.778 J

Solution:

As per the question:

Height of circular, H = 0.15 m

Radius of the circular arc, R = 0.27 m

Mass of the bullet,
`m_(1) = 30\ g = 0.03\ kg`

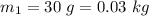
Mass of the block,
`m_(1) = 5.29\ kg`

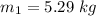
Now,

By using the law of conservation of energy:

Kinetic Energy, KE = Potential Energy, U

Thus

`(1)/(2)(m_(1) + m_(2))v^(2) = (m_(1) + m_(2))gH`

`v = √(2gH)= √(2* 9.8* 0.15) = 1.71\ m/s`

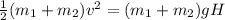
Now, the total energy of the system after collision:

`KE = (1)/(2)(m_(1) + m_(2))v^(2)`

`KE = (1)/(2)(0.03 + 5.29)* 1.71^(2) = 7.778\ J`