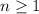Question

Identify each sequence as arithmetic or geometric. Explain your answer, and write an explicit formula for the

sequence.
c. − 1 / 2, − 3 / 2, − 5 / 2, − 7 / 2, …

Answer 1

Arithmetic sequence

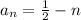`a_n=(1)/(2)-n` for
`n\geq 1`

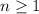
Explanation:

We are given that a sequence

`-(1)/(2),-(3)/(2),-(5)/(2),-(7)/(2),...`

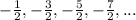
We have to identify the sequence as arithmetic or geometric and write an explicit formula .

`a_1=-(1)/(2)`

`a_2=-(3)/(2)`

`a_3=-(5)/(2)`

`a_4=-(7)/(2)`

`d_1=a_2-a_1=(-3)/(2)+(1)/(2)=-1`

`d_2=a_3-a_2=-(5)/(2)+(3)/(2)=-1`

`d_1=d_2=-1`

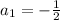
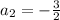
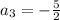
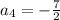
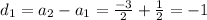
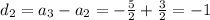
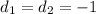
When the difference of consecutive terms is constant then the sequence is an arithmetic.

Hence, the sequence is an arithmetic.

`a_n=a+(n-1)d`

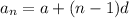
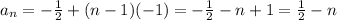`a_n=-(1)/(2)+(n-1)(-1)=-(1)/(2)-n+1=(1)/(2)-n` for
`n\geq 1`