Question

A sample is obtained from a population with m = 100 and s = 20. Which of the following samples would produce the most extreme z-score? A sample of n = 25 scores with M = 102 A sample of n = 100 scores with M = 102 A sample of n = 25 scores with M = 104 A sample of n = 100 scores with M = 104

Answer 1

A sample of n = 100 scores with M = 104 gives the most extreme z-score.

Explanation:

The difference between sample mean and population mean is (Standard Error of the Mean) can be written by the formula

SE=(M-m)=
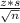`(z*s)/(√(n))` where M is the sample mean, m is the population mean, z is the z-score, s is the population standard deviation, n is the size of the sample. From this we can find out that

z=(M-m)×
`(√(n) )/(s)`

`\\`

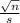
• A sample of n = 25 scores with M = 102 gives

z=(102-100)×
`(√(25) )/(20)` =0.5

• A sample of n = 100 scores with M = 102 gives

z=(102-100)×
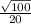`(√(100) )/(20)` =1

• A sample of n = 25 scores with M = 104 gives

z=(104-100)×
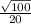`(√(25) )/(20)` =1

• A sample of n = 100 scores with M = 104 gives

z=(104-100)×
`(√(100) )/(20)` =2