Question

The following data gives the speeds (in mph), as measured by radar, of 10 cars traveling north on I-15. 76 72 80 68 76 74 71 78 82 65 Assuming that the speeds of all cars traveling on this highway have a normal distribution, construct a 90% confidence interval for the mean speed of all cars traveling on this highway. Round to 3 decimal places.

Answer 1

71.123 mph ≤ μ ≤ 77.277 mph

Explanation:

Taking into account that the speed of all cars traveling on this highway have a normal distribution and we can only know the mean and the standard deviation of the sample, the confidence interval for the mean is calculated as:

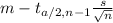`m-t_(a/2,n-1)(s)/(√(n) )` ≤ μ ≤
`m+t_(a/2,n-1)(s)/(√(n) )`

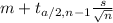
Where m is the mean of the sample, s is the standard deviation of the sample, n is the size of the sample, μ is the mean speed of all cars, and
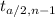`t_(a/2,n-1)` is the number for t-student distribution where a/2 is the amount of area in one tail and n-1 are the degrees of freedom.

the mean and the standard deviation of the sample are equal to 74.2 and 5.3083 respectively, the size of the sample is 10, the distribution t- student has 9 degrees of freedom and the value of a is 10%.

So, if we replace m by 74.2, s by 5.3083, n by 10 and
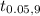`t_(0.05,9)` by 1.8331, we get that the 90% confidence interval for the mean speed is:

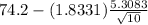`74.2-(1.8331)(5.3083)/(√(10) )` ≤ μ ≤
`74.2+(1.8331)(5.3083)/(√(10) )`

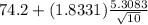
74.2 - 3.077 ≤ μ ≤ 74.2 + 3.077

71.123 ≤ μ ≤ 77.277