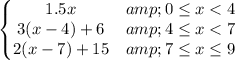Question

There was no snow on the ground when it started falling at midnight at a constant rate of 1.5 inches per hour. At

4:00 a.m., it starting falling at a constant rate of 3 inches per hour, and then from 7:00 a.m. to 9:00 a.m., snow was
falling at a constant rate of 2 inches per hour. It stopped snowing at 9:00 a.m. (Note: This problem models snow
falling by a constant rate during each time period. In reality, the snowfall rate might be very close to constant but is
unlikely to be perfectly uniform throughout any given time period.)
a. Write a piecewise linear function that models the depth of snow as a function of time since midnight.

Answer 1

The required piece-wise linear function is

`\left\{\begin{matrix}1.5x & 0\leq x<4\\ 3(x-4)+6 & 4\leq x<7\\ 2(x-7)+15 & 7\leq x\leq 9\end{matrix}\right.`

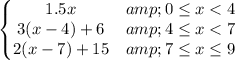
Explanation:

Consider the provided information.

Let x represents the number of hours and S(x) represents the depth of snow.

There was no snow on the ground when it started falling at midnight at a constant rate of 1.5 inches per.

That means the depth of snow will be:

`S(x)=1.5x\ \ \ 0\leq x< 4`

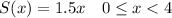
At 4:00 a.m., it starting falling at a constant rate of 3 inches per hour,

From mid night to 4:00 a.m the depth of snow will be 1.5×4=6 inches.

If we want to calculate the total depth of snow from midnight to 7:00 am we need to add 6 inches in 3(x-4) where 4≤x<7

Therefore,

`S(x)=3(x-4)+6\ \ \ 4\leq x<7`

7:00 a.m. to 9:00 a.m., snow was falling at a constant rate of 2 inches per hour.

From mid night to 7:00 a.m the depth of snow will be 3(7-4)+6=15 inches.

If we want to calculate the total depth of snow from midnight to 9:00 am we need to add 15 inches in 2(x-7) where 7≤x≤9

`S(x)=2(x-7)+15\ \ \ 7\leq x\leq 9`

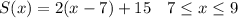
Therefore, the required piece-wise linear function is

`\left\{\begin{matrix}1.5x & 0\leq x<4\\ 3(x-4)+6 & 4\leq x<7\\ 2(x-7)+15 & 7\leq x\leq 9\end{matrix}\right.`