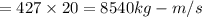Answer:8540 kg-g/s
Step-by-step explanation:
Given
mass of blue car
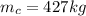
velocity of blue car
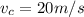
mass of the truck
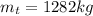
speed of truck
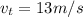
After collision they stick and lock together
Let v be the velocity of combined system at angle \theta from vertical
Conserving momentum in east direction
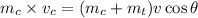
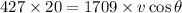 ------1
------1
Conserving Momentum in Y direction
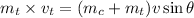
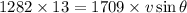 -------2
-------2
squaring and then adding 1 & 2 we get
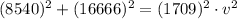
v=10.95 m/s
initial momentum of car