Question

A population of 950 bacteria grows continuously at a rate of 4.75% per day. (a) Write an exponential function, N(t), that represents the bacterial population after t days and explain the reason for your choice of base. (b) Determine the bacterial population after 36 hours, to the nearest bacterium.

Answer 1

(a)
`N(t)=950e^(0.0475t)`.

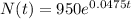(b) 1020

Explanation:

The continuous exponential growth model is defined as

`y=ae^(kt)`

where, a is initial value, k is growth rate and t is time.

(a)

Initial population: a = 950

Continuous growth rate : k = 4.75% = 0.0475

So, the exponential function, N(t), that represents the bacterial population after t days is

`N(t)=950e^(0.0475t)`

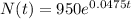
Base is e because the population growth is continuous.

Therefore, the required model is
`N(t)=950e^(0.0475t)` .

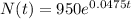(b)

We need to find the bacterial population after 36 hours, to the nearest bacterium.

24 hours = 1 day

36 hours = 36/24 = 1.5 day

Substitute t=1.5 in the above equation.

`y=950e^(0.0475(1.5))`

`y=1020.15717199`

`y=1020`

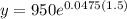
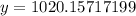
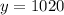
Therefore, the bacterial population after 36 hours is 1020.