Answer: 0.0227502
Explanation:
Let x denote the random variable that represents the mileage of SUV.
As per given we have,
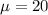
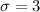
sample size : n= 36
We assume that the mileage of SUV is normally distributed.
Z-score value corresponds to x= 21.0,
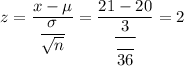
Using standard z-value table ,
The probability that the sample average will be over 21.0 mpg:-
P(X>35)=P(z>2)=1-P(z<2)=1-0.9772498=0.0227502
Hence, the required probability = 0.0227502