Question

2. Exercise 18, 19 Page 188. Determine if the following statements are true. If a statement is true, give a proof from the definitions. If a statement is false, give a counterexample.

(a) If r and s are rational numbers, then (r+s)/2 is rational.
(b) For all real numbers a and b, if a < b then a < (a+b)/2 < b

Answer 1

A AND B

Explanation:

Answer 2

a. true b. true

Explanation:

(a) If r and s are rational numbers, then (r+s)/2 is rational.

true

rational numbers can be expresed as fractions

let be r=a/b and s=c/d being a,b,c,d integer numbers

`(r+s)/(2) =((a)/(b)+(c)/(d) )/(2) =((da+bc)/(bd) )/(2) =(da+bc)/(2bd)`

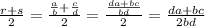
d.a=e is an integer number because it's the product of two integers

b.c=f is an integer number because it's the product of two integers

e+f=g is an integer number because it's the sum of two integers

b.d=h is an integer number because it's the product of two integers

2.h=i is an integer number because it's the product of two integers

g/i=j is an integer number because it's the quotient of two integers

then

`(r+s)/(2) =((a)/(b)+(c)/(d) )/(2) =((da+bc)/(bd) )/(2) =(da+bc)/(2bd)=(e+f)/(2h) =(g)/(i) =j`

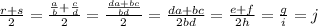
(b) For all real numbers a and b, if a < b then a < (a+b)/2 < b

true

`a < (a+b)/2 < b`

`2a < (a+b) < 2b`

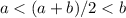
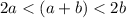
lets analyze 2a < (a+b)

`2a < (a+b) \\2a-a < (a+b)-a\\a < b`

then 2a < (a+b) is true

lets analyze (a+b) < 2b

`(a+b) < 2b\\(a+b)-b < 2b-b\\a< b`

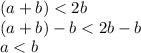
then (a+b) < 2b is true