Question

The probability that a student has a Visa card (event V) is .73. The probability that a student has a MasterCard (event M) is .14. The probability that a student has both cards is .03. (a) Find the probability that a student has either a Visa card or a MasterCard. (Round your answer to 2 decimal places.)

Answer 1

Explanation:

Answer 2

The probability that a student has either a Visa card or a MasterCard is 0.84.

Explanation:

Given : The probability that a student has a Visa card (event V) is 0.73. The probability that a student has a MasterCard (event M) is 0.14. The probability that a student has both cards is 0.03.

To find : The probability that a student has either a Visa card or a MasterCard ?

Solution :

The probability that a student has a visa card(event V) is P(V)= 0.73

The probability that a student has a MasterCard (event M) is P(M)= 0.14

The probability that a student has both cards is
`P(V \cap M)=0.03`

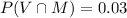
Probability that a student has either a Visa card or a Master Card is given by,

`P(V \cup M) = P(V) + P(M) - P(V\cap M)`

`P(V \cup M) = 0.73+ 0.14- 0.03`

`P(V \cup M) =0.87- 0.03`

`P(V \cup M) =0.84`

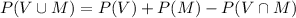
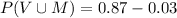
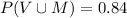
Therefore, the probability that a student has either a Visa card or a MasterCard is 0.84.