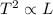Question

The time period T of a simple pendulum is given by the relation

T=2pi sq rt L/G

, where L is the length of the pendulum and g is the gravitational field at the place. From the above relation, we can say that:


T ∝ g


T ∝ L


T2 ∝ g


T2 ∝ L

Answer 1

T2 ∝ L

Step-by-step explanation:

took the test and got it right

Answer 2

`T^2 \propto L`

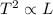
Step-by-step explanation:

The period of a simple pendulum is given by:

`T=2\pi \sqrt{(L)/(g)}`

where

L is the length of the pendulum

g is the acceleration of gravity

From this equation we can write

`T\propto √(L)\\T\propto (1)/(√(g))`

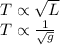
Taking the square of this equation, we get:

`T^2 = (2\pi)^2 (L)/(g)`

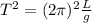
So we see that
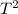`T^2` is proportional to L and inversely proportional to g. So, we can write:

`T^2 \propto L\\T^2 \propto (1)/(g)`

So the only correct option is

`T^2 \propto L`