Question

I need help ASAP!

Identify the number and type of solutions for the equation x^2 − 7x + 3 = 0.

Answer 1

i) Equation can have exactly 2 zeroes.

ii) Both the zeroes will be real and distinctive.

Explanation:

`x^(2) - 7x + 3` is the given equation.

It is of the form of quadratic equation
`a^(2) + bx + c` and highest degree of the polynomial is 2.

Now, FUNDAMENTAL THEOREM OF ALGEBRA

If P(x) is a polynomial of degree n ≥ 1, then P(x) = 0 has exactly n roots, including multiple and complex roots.

So, the equation can have exact 2 zeroes (roots).

Also, find discriminant D =
`b^(2)  - 4ac = (-7)^(2)  - 4(1)(3) = 49 - 12 = 37`

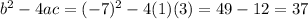
⇒ D = 37

Here, since D > 0, So both the roots will be real and distinctive.