Question

A translation moves A(2,3) onto An (4,8) what are the coordinates of B’ the image of B(4,6) under the same translation

Answer 1

Given the translation of point A, the coordinates of B' under the same translation are (6, 11).

Determining the coordinates of B'

If point A(2,3) is translated onto point A'(4,8), find the translation vector by subtracting the coordinates of A' from A:

Translation vector = (x-coordinate of A' - x-coordinate of A, y-coordinate of A' - y-coordinate of A)

= (4 - 2, 8 - 3)

= (2, 5)

Now, apply the same translation vector to point B(4,6) to find the image B':

Coordinates of B' = (x-coordinate of B + x-coordinate of the translation vector, y-coordinate of B + y-coordinate of the translation vector)

= (4 + 2, 6 + 5)

= (6, 11)

Therefore, the coordinates of B' under the same translation are (6, 11).

Answer 2

(1.931, 5.172)

Explanation:

Given that the image of A(2,3) is A'(4,8).

Now, the equation of straight line passing through A and A' is

`((y-3))/((8-3)) =((x-2))/((4-2))`

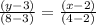
⇒(y-3) =2/5(x-2)

⇒y =2x/5 +(3-4/5)

⇒ y= 2x/5 +11/5 ......(1)

And the mid point of A and A' is (
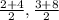`(2+4)/(2),(3+8)/(2)`)≡(3,5.5)

Now, Equation of perpendicular straight line to (1), is given by

y= -5x/2 +c ....... (2) {Since, the product of slopes of two mutually perpendicular straight line is always -1}

Now, equation (2) passes through (3, 5.5) point.

Hence, 5.5 =-5×3/2 +c, ⇒ c=13.

So, the mirror straight line is y=-5x/2 +13 ......(3)

Now, parallel straight line to (1), is given by

y=2x/5 +c' and the point (4,6) satisfies it.

So, 6=2×4/5 +c', ⇒ c' =22/5.

So, the equation becomes y=2x/5 +22/5 ........ (4)

Now, solving equations (3) and (4) we get

-5x/2 +13=2x/5 +22/5

⇒ 29x/10 =43/5

⇒ x=86/29=2.965 and from (4), we get y=2/5(86/29) +22/5 =172/145+22/5 =5.586

Hence, the point becomes (2.965, 5.586)

If (h,k) be the required image, then (2.965, 5.586) point must be the mid point of (h,k) and (4,6).

Therefore, (h+4)/2 =2.965 ⇒ h= 1.931 and (k+6)/2 =5.586, ⇒k=5.172.

So, the image point is (1.931, 5.172). (Answer)