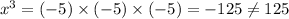Question

There is an error in the work shown below. Explain the error and provide a correct solution. X cubed=125 cubed root of x cubed= cubed root of 125 x=5 and x=-5

Answer 1

x= 5 is the ONLY solution for the given expression and x≠ (-5)

Explanation:

The given expression can be written as the following

`x^(3)  = {125}  \sqrt[3]{x^(3) }  = \sqrt[3]{125}`

which implies x = 5 and x = -5

Now, here the given is
`x^(3)  = 125`

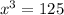
and we need to find the value of x.

So, we cube root both the sides.

We get,
`\sqrt[3]{x^(3) }  = \sqrt[3]{125 }`

now, 125 = 5 x 5 x 5 =
`(5)^(3)`

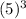
So, given expression becomes
`\sqrt[3]{x^(3) }  = \sqrt[3]{(5)^(3)}`

or, on simplifying, we get

`x^ {3 * {(1)/(3) }} = 5^ {3 * {(1)/(3) }}`

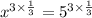
or, x = 5

hence, x= 5 is the ONLY solution for the given expression.

Because if x = -5 then
`x^(3)  = (- 5) * (-5) * (-5) = -125 \\eq  125`