Answer:
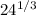 =
=
![\sqrt[3]{24}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/k4it174rt5hr2weismv80l7z4nrwfhn24h.png) or
or
![2\sqrt[3]{3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pwzmgwkooa27e0g76799t8f3b9sqmyqbh2.png)
Explanation:
We will apply one of the laws of indices which states
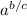 =
=
^b](https://img.qammunity.org/2020/formulas/mathematics/middle-school/46r0vndl915p10a8doi5r2mncacwumrkbk.png)
So from the question given, 24 superscript one-third =
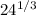
by comparison, a= 24, b = 1, and c = 3
Applying the law I stated above
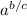 =
=
^b](https://img.qammunity.org/2020/formulas/mathematics/middle-school/46r0vndl915p10a8doi5r2mncacwumrkbk.png)
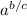 =
=
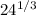 =
=
^(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yzyaptt5rxpkvdv3uw5tmkiec8fzmso9il.png)
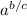 =
=
^(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pa58d5ekrljlhmokqnvrvj52wc63jnu75z.png)
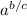 =
=
^(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/zm07bb3hkvv10zev7t4u6wo6dqz5pz7bad.png) ×
×
^(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7ao8cjcecbqjxnk17ipf8xd79qj0344s9w.png)
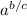 = 2 ×
= 2 ×
^(1)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/7ao8cjcecbqjxnk17ipf8xd79qj0344s9w.png)
![2\sqrt[3]{3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pwzmgwkooa27e0g76799t8f3b9sqmyqbh2.png) (superscript 1 is removed because any value raised to the power of one is equal to that value) or
(superscript 1 is removed because any value raised to the power of one is equal to that value) or
![\sqrt[3]{24}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/k4it174rt5hr2weismv80l7z4nrwfhn24h.png)
Therefore the expression will be
![2\sqrt[3]{3}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pwzmgwkooa27e0g76799t8f3b9sqmyqbh2.png) or
or
![\sqrt[3]{24}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/k4it174rt5hr2weismv80l7z4nrwfhn24h.png) ---- Answer
---- Answer