Question

Triangle A B C has points (negative 3, negative 1), (negative 1, 2), and (negative 5, 3). Triangle R S T has points (1, 1), (3, 4), and (5, 0). Triangle RST is rotated 180° about the origin, and then translated up 3 units. Which congruency statement describes the figures? ΔRST ≅ ΔACB ΔRST ≅ ΔABC ΔRST ≅ ΔBCA ΔRST ≅ ΔBAC

Answer 1

ΔRST ≅ ΔBAC

Explanation:

took the test on edge

Answer 2

ΔRST ≅ ΔBAC

Explanation:

Consider triangles ABC with vertices A(-3,-1), B(-1,2) and C(-5,3) and RST with vertices R(1,1), S(3,4) and T(5,0).

The rotation by 180° about the origin has the rule

`(x,y)\rightarrow (-x,-y)`

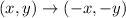
So,

• 
  `R(1,1)\rightarrow R'(-1,-1);`
• 
  `S'(3,4)\rightarrow S'(-3,-4);`
• 
  `T(5,0)\rightarrow T'(-5,0).`

Translation 3 units up has the rule

`(x,y)\rightarrow (x,y+3)`

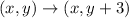
Hence

• 
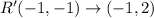  `R'(-1,-1)\rightarrow (-1,2)` that is exactly point B;
• 
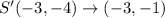  `S'(-3,-4)\rightarrow (-3,-1)` that is exactly point A;
• 
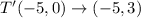  `T'(-5,0)\rightarrow (-5,3)` that is exactly points C.

Therefore, triangle RST is congruent to BAC.