Question

Consider the radical equation (3√6-x)+4=-8. Explain why the calculation in Problem 1 does not produce a solution to the equation.

Answer 1

See explanation below

Explanation:

First we will solve the radical equation (which I guess was problem 1),

Let's start by simplifying it:

`3√(6-x)+4=-8\\ 3√(6-x)=-8-4\\ 3√(6-x)=-12\\√(6-x)=-4`

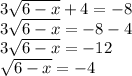
Now we will solve the equation by squaring both sides of the equation:

`√(6-x) =-4\\6-x=-4^(2) \\6-x=16\\-x=16-6\\-x=10\\x=-10`

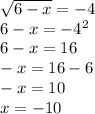
So the calculation for x was that x = -10

However, this does not produce a solution to the equation: When we plug this value into the radical equation we get:

`3√(6-x) +4= -8\\3√(6-(-10)) +4=-8\\3√(16)+4 = -8\\ 3(4)+4 = -8\\12 + 4 = -8`

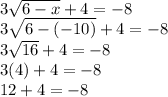
This happens because when we first squared both sides of the equation in the first part of the problem we missed one value for x (remember that all roots have 2 answers, a positive one and a negative one) while squares are always positive.

When we squared the root, we missed one value for x and that is why the calculation does not produce a solution to the equation.