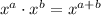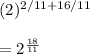Answer:
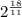
Explanation:
The given expression is
![\sqrt[11]{y^2z^4}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2pj5pwqdt9eki6tkrhnbctyxovkwzxn8tl.png)
The exponent property
![\sqrt[n]{x^ay^b}=x^(a/n)y^(b/n)](https://img.qammunity.org/2020/formulas/mathematics/high-school/w8h9hes4edkpnlu7ry1mgxcj16u5dhlw3z.png)
Applying this exponent property, we have
![\sqrt[11]{y^2z^4}\\\\=y^(2/11)z^(4/11)](https://img.qammunity.org/2020/formulas/mathematics/high-school/em7d1ylpyansldc2jmb7nukq57rhvhz284.png)
Now, the given numeric values are x = 9, y= 8, and z= 16
On substituting these values in the simplified expression, we get
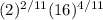
This can be further simplified by writing
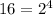

Now, applying the product rule of exponent: