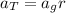Question

An object executes circular motion with constant speed whenever a net force of constant magnitude acts perpendicular to the velocity. What happens to the speed if the force is not perpendicular to the velocity?

Answer 1

Answer: The speed is not constant and the object is performing a non uniform circular motion

Step-by-step explanation:

Let's begin by explaining that the centripetal force is proportional to the centripetal acceleration
`a_(c)` of an object moving in circular motion is given by the following equation:

`a_(c)=(V^(2))/(r)`

Where:

`V` is the velocity

`r` is the radius of the circle

In uniform circular motion, the centripetal acceleration vector is always perpendicular to the velocity vector, hence, the speed (the magnitude of velocity vector) is constant.

However, if a component of the centripetal acceleration vector is not perpendicular (is parallel to the velocity vector): the speed is not constant, the net force acting on the object will not be perpendicular to its motion and we will be dealing with non uniform circular motion.

It is important to note that in this situation the motion needs a tangential force, as well. Being the tangential acceleration
`a_(T)` proportional to
`r` and the angular acceleration
`a_(g)`:

`a_(T)=a_(g) r`