Answer:
Midpoint is 1 + 2i
Explanation:
Given that endpoints are
 and
and
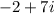 . The definition of complex number is that
. The definition of complex number is that
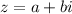 where a is real part and b is imaginary part. In coordinate plane, the equation can be represented as a position vector with initial as origin point and final as (a,b).
where a is real part and b is imaginary part. In coordinate plane, the equation can be represented as a position vector with initial as origin point and final as (a,b).
So (a,b) in complex number represents the equation
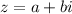 . If we are given two complex equations:
. If we are given two complex equations:
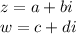
Then we can rewrite both as in:
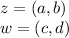
From the property:
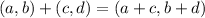
Since we are finding midpoint, we'd have to divide both components by 2. So our formula will be:
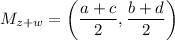
Determine that:
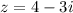 so a = 4 and b = -3
so a = 4 and b = -3
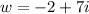 so c = -2 and d = 7
so c = -2 and d = 7
Therefore:
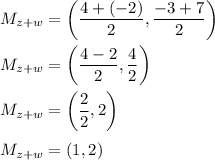
So our midpoint will be at (1,2) which then can be rewritten back to 1 + 2i through position vector.