Answer:
Speed is 1.73 m/s and the angle is
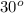 below the x-axis
below the x-axis
Explanation:
From the law of conservation of linear momentum, this collision is considered elastic hence we apply the principle on both x-axis and y-axis
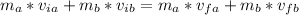 where
where
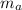 and
and
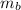 are masses of pucks A and B respectively,
are masses of pucks A and B respectively,
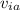 and
and
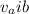 are initial velocities of pucks A and B respectively, and
are initial velocities of pucks A and B respectively, and
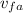 and
and
 are final velocities of pucks A and B respectively, From the law of conservation of linear momentum, this collision is considered elastic hence we apply the principle on both x-axis and y-axis
are final velocities of pucks A and B respectively, From the law of conservation of linear momentum, this collision is considered elastic hence we apply the principle on both x-axis and y-axis

Since the pucks are identical, the masses are same hence the equation can be written as
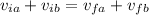
The final velocity of puck A is found by
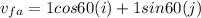
The final velocity of puck B is found by
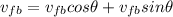
Since initial velocity of puck B is zero, the law of conservation of linear momentum along x axis will be
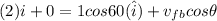
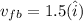
On y-axis

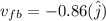
Magnitude after collision=
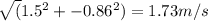
Direction=
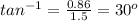
The angle is
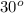 below the x-axis and speed of puck B after collision is 1.73 m/s
below the x-axis and speed of puck B after collision is 1.73 m/s