Answer: get smaller
Step-by-step explanation:
Parallax is the angle formed by the observation lines to a very distant object from two separated points.
The procedure to measure this distance in the case of a star, is based on observing it from two different places far away from each other, and then through trigonometry reach to the following relationship:
 (1)
(1)
Where:
 is the distance from Earth to the observed star (in Parsecs
is the distance from Earth to the observed star (in Parsecs
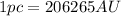 )
)
 is the earth-sun distance that is equivalent to an astronomical unit (1AU=150000000km)
is the earth-sun distance that is equivalent to an astronomical unit (1AU=150000000km)
 is the angle of the parallax (in arc seconds
is the angle of the parallax (in arc seconds
 )
)
Now, the distance to an object (measured in parsecs) is the reciprocal of the parallax (measured in arcseconds). Then, in its simplified mode, the stellar parallax is given by the following equation:
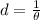 (2)
(2)
As we can see, there is an inverse relation between the distance
 and the parallax
and the parallax
 :
:
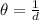 (3)
(3)
Hence, if the distance is increased by a factor of 10, the parallax is decreased by a factor of 10.
In other words, the parallax angle gets smaller.